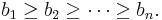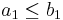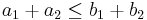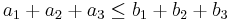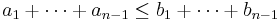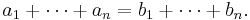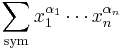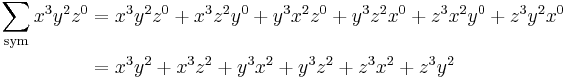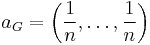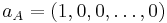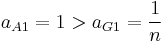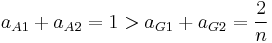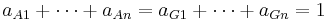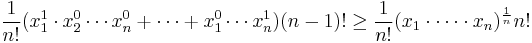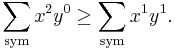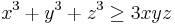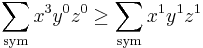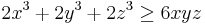Muirhead's inequality
In mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means.
Contents |
Preliminary definitions
The "a-mean"
define the "a-mean" [a] of nonnegative real numbers x1, ..., xn by
where the sum extends over all permutations σ of { 1, ..., n }.
In case a = (1, 0, ..., 0), this is just the ordinary arithmetic mean of x1, ..., xn. In case a = (1/n, ..., 1/n), it is the geometric mean of x1, ..., xn. (When n = 2, this is the Heinz mean.)
Doubly stochastic matrices
An n × n matrix P is doubly stochastic precisely if both P and its transpose PT are stochastic matrices. A stochastic matrix is a square matrix of nonnegative real entries in which the sum of the entries in each column is 1. Thus, a doubly stochastic matrix is a square matrix of nonnegative real entries in which the sum of the entries in each row and the sum of the entries in each column is 1.
The inequality
Muirhead's inequality states that [a] ≤ [b] for all xi ≥ 0 if and only if there is some doubly stochastic matrix P for which a = Pb.
The proof makes use of the fact that every doubly stochastic matrix is a weighted average of permutation matrices (Birkhoff-von Neumann theorem).
Another equivalent condition
Because of the symmetry of the sum, no generality is lost by sorting the exponents into decreasing order:
Then the existence of a doubly stochastic matrix P such that a = Pb is equivalent to the following system of inequalities:
(The last one is an equality; the others are weak inequalities.)
The sequence  is said to majorize the sequence
is said to majorize the sequence  .
.
Symmetric sum-notation tricks
It is useful to use a kind of special notation for the sums. A success in reducing an inequality in this form means that the only condition for testing it is to verify whether one exponent sequence ( ) majorizes the other one.
) majorizes the other one.
This notation requires developing every permutation, developing an expression made of n! monomials, for instance:
Deriving the arithmetic-geometric mean inequality
Let
we have
then
- [aA] ≥ [aG]
which is
yielding the inequality.
Examples
Suppose you want to prove that x2 + y2 ≥ 2xy by using bunching (Muirhead's inequality): We transform it in the symmetric-sum notation:
The sequence (2, 0) majorizes the sequence (1, 1), thus the inequality holds by bunching. Again,
which yields
the sequence (3, 0, 0) majorizes the sequence (1, 1, 1), thus the inequality holds by bunching.
References
- Biography of R.F. Muirhead
- Combinatorial Theory by John N. Guidi, based on lectures given by Gian-Carlo Rota in 1998, MIT Copy Technology Center, 2002.
- Kiran Kedlaya's guide to solving inequalities at [1].
- Reference on PlanetMath (Muirhead's theorem)
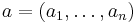
![[a]={1 \over n!}\sum_\sigma x_{\sigma_1}^{a_1}\cdots x_{\sigma_n}^{a_n},](/2012-wikipedia_en_all_nopic_01_2012/I/7aa719c59d95ac6c3055cca22ecfc18f.png)